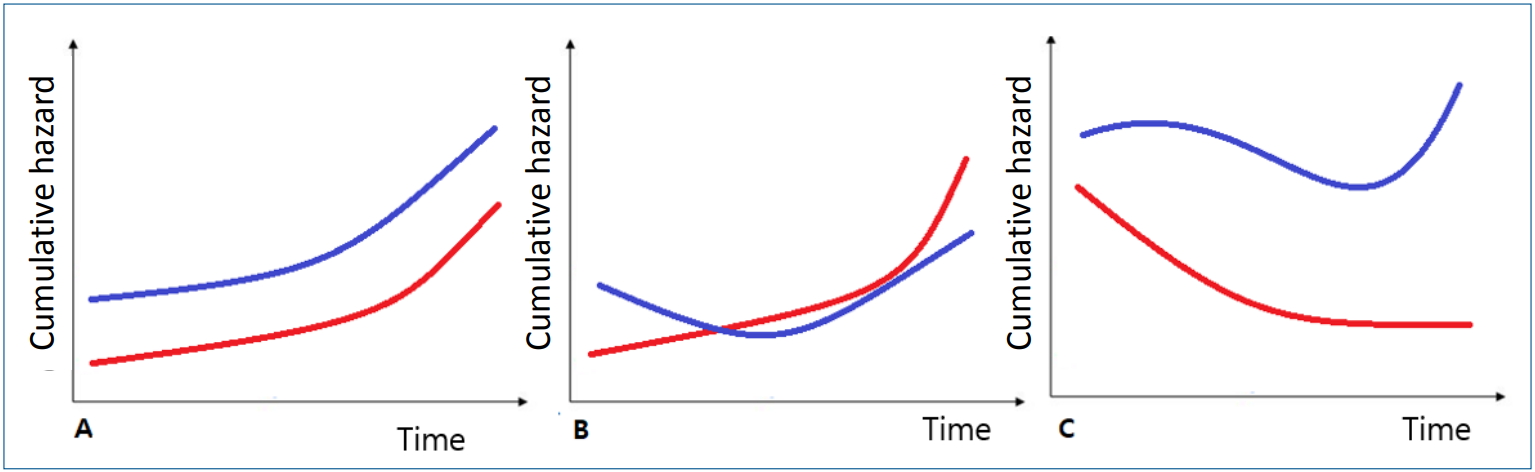
The survival analysis plays a vital role in analyzing time-toevent data [1,2]. Among several proposed prediction models, the semiparametric Cox regression model has gained widespread use in the field of medical research because no distribution assumption is required of the probability of survival times and it usually fits the data well [2-4]. The “semiparametric” term is used in the Cox model since it does not assume any distribution of survival times (nonparametric), but it estimates the regression coefficient based on the model (parametric). The risk of an independent variable is constantly proportion, but the relative risk does not change over time (Fig. 1).
However, under certain circumstances, parametric models lead to more efficient and precise estimates than nonparametric models [1,2]. A distributional assumption should be required for a parametric model. If the distributional assumption is valid, a parametric model has smaller standard errors of the estimates, considers the influence of other correlative factors, and achieves a more precise and accurate result. Importantly, the failure to use an appropriate model potentially leads to inaccurate and misleading interpretations. Several studies have compared various survival regression methods to identify the most suitable model [3-5]. Akaike’s Information Criterion (AIC) is commonly used to evaluate the goodness of fit [3,6]. The smaller the AIC value, the better the fitness. Other methods, such as Cox-Snell residuals and receiver operating characteristic curves, are also used to assess model accuracy [5]. Cox-Snell residuals assess model fitness; the less deviation of residuals from the bisector, the more appropriate the model’s fitness [6]. However, AIC indicates only the quality relative to other models, not the absolute quality of each model. Therefore, it is appropriate to identify the best models that meet the requirements for assumption.
Kheiry et al. [7] investigated the impact of strategies that affect the length of stay (LOS) in a neonatal intensive care unit (NICU) using semiparametric and parametric Cox models. They did not value the absolute of each model for the purpose of finding the best fitting model explaining the data. Performing a detailed analysis of factors affecting LOS provides insight into neonatal care to improve survival rates and helps counsel parents [3,8,9]. A prolonged LOS reportedly increases the newborn morbidity rate and risk of infection [10]. This study showed that the parametric exponential model provided a better fit for determining the factors associated with neonatal LOS in a NICU based on AIC. They concluded that breast-feeding and the availability of a central venous catheter were associated with a shorter LOS. In contrast, phototherapy, acute renal failure, and mechanical ventilation are associated with a longer LOS.
However, an LOS analysis requires some considerations. As the author mentioned, the parametric model may not be appropriate in the presence of significant censoring data. Due to the large sample size and maximum follow-up time for each patient, they assumed the distribution of variables is normal and fully respected. In this paper, death was used as an event and discharge was used as censoring. They had 110 death events and 496 discharges as censoring. The high censoring rate was one of the limitations of this study. Reza et al. [5] showed 2 critical features of LOS data—nonnormality and censorship—so classic models are not suitable for LOS. Moreover, the present paper did not mention checks for an appropriate assumption for each model. All subjects who were admitted for more than 24 hours were analyzed as the target population, so proper exclusion seems necessary. The inclusion of infants who died can complicate an LOS analysis. Factors affecting disease severity may lead to premature death and a shorter LOS, leading to confusion. Abnormal causes of discharge, such as referral for further higher-level medical services, should also be considered. This study did not analyze or adjust for gestational age. Newborn survival is influenced by gestational age and birth weight [11]. More immature babies require extended hospital stays, and an appropriate hospital stay can help stabilize their condition and reduce readmission rates. Prolonged hospital stays for palliative treatment may also affect the analysis [9] Therefore, various confounding factors that affect LOS, such as gestational age and hospital care level, should be considered together. Analyzing the factors affecting LOS with these considerations can help improve newborn care quality.
Due to these confounding factors, this LOS analysis was not simple. The future consideration of gestational age and proper exclusions will obtain more useful information.





 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link PubMed
PubMed Download Citation
Download Citation