Warning: fopen(/home/virtual/pediatrics/journal/upload/ip_log/ip_log_2023-09.txt) [function.fopen]: failed to open stream: Permission denied in /home/virtual/pediatrics/journal/ip_info/view_data.php on line 82

Warning: fwrite(): supplied argument is not a valid stream resource in /home/virtual/pediatrics/journal/ip_info/view_data.php on line 83
Understanding the genetics of systemic lupus erythematosus using Bayesian statistics and gene network analysis


Your browser does not support the NLM PubReader view.

Go to this page to see a list of supporting browsers.

Understanding the genetics of systemic lupus erythematosus using Bayesian statistics and gene network analysis

Article information

Clin Exp Pediatr. 2021;64(5):208-222
Publication date (electronic) : 2020 July 15
doi : https://doi.org/10.3345/cep.2020.00633
Seoung Wan Nam, MD, PhD1,*orcid_icon, Kwang Seob Lee, MD2,*, Jae Won Yang, MD, PhD3,*, Younhee Ko, PhD4, Michael Eisenhut, MD, FRCP, FRCPCH, DTM&H5, Keum Hwa Lee, MD, MS6,7,8, Jae Il Shin, MD, PhD,6,7,8orcid_icon, Andreas Kronbichler, MD, PhD,9orcid_icon
1Department of Rheumatology, Wonju Severance Christian Hospital, Yonsei University Wonju College of Medicine, Wonju, Korea
2Severance Hospital, Yonsei University College of Medicine, Seoul, Korea
3Department of Nephrology, Yonsei University Wonju College of Medicine, Wonju, Korea
4Division of Biomedical Engineering, Hankuk University of Foreign Studies, Yongin, Korea
5Department of Pediatrics, Luton & Dunstable University Hospital NHS Foundation Trust, Luton, UK
6Department of Pediatrics, Yonsei University College of Medicine, Seoul, Korea
7Division of Pediatric Nephrology, Severance Children’s Hospital, Seoul, Korea
8Institute of Kidney Disease Research, Yonsei University College of Medicine, Seoul, Korea
9Department of Internal Medicine IV (Nephrology and Hypertension), Medical University Innsbruck, Innsbruck, Austria
Corresponding author: Jae Il Shin, MD, PhD. Department of Pediatrics, Yonsei University College of Medicine, Yonsei-ro 50, Seodaemun-gu, Seoul 03722, Korea E-mail: shinji@yuhs.ac
Co-corresponding author: Andreas Kronbichler, MD, PhD. Department of Internal Medicine IV (Nephrology and Hypertension), Medical University Innsbruck, Anichstrasse 35, 6020 Innsbruck, Austria E-mail: andreas.kronbichler@i-med.ac.at
*

These authors contributed equally to this study as co-first authors.

Received 2020 April 11; Revised 2020 June 19; Accepted 2020 June 23.

Abstract

The publication of genetic epidemiology meta-analyses has increased rapidly, but it has been suggested that many of the statistically significant results are false positive. In addition, most such meta-analyses have been redundant, duplicate, and erroneous, leading to research waste. In addition, since most claimed candidate gene associations were false-positives, correctly interpreting the published results is important. In this review, we emphasize the importance of interpreting the results of genetic epidemiology meta-analyses using Bayesian statistics and gene network analysis, which could be applied in other diseases.

Keywords: Systemic lupus erythematosus; False-positive report probability; Bayesian false-discovery probability; STRING database; Protein-protein interaction

Key message

• Bayesian false-discovery probability and false-positive report probability are the 2 major Bayesian methods used to evaluate noteworthiness of a genetic variant.

• Application of stricter P value is needed to confirm statistical significance in meta-analyses.

• Gene network analysis of noteworthy genetic variants shows a blueprint of the genetic background in complex diseases.

Introduction

Although the publication of meta-analyses has rapidly increased, researchers have started to determine that many of the statistically significant results are false-positive [1,2]. Most such meta-analyses have redundant duplicate topics and many errors [1,3]. Although there has been an impressive increase in meta-analyses from China, particularly those on genetic associations, most claimed candidate gene associations are likely false-positives, suggesting an urgent global need to incorporate genome-wide data and state-of-the art statistical inferences to avoid a flood of false-positive genetic meta-analyses. In this review, we emphasize the importance of discerning meaningful studies and interpreting their results using Bayesian statistics and gene network analysis. For this purpose, we adopted and reanalyzed significant genes from our previously published systemic meta-analyses of genetic association studies of systemic lupus erythematosus (SLE) as an example [4].

Current understanding of genetic associations with “noteworthiness”

The traditional interpretation of association studies was labeled as statistically significant by the chosen P value of less than 0.05 [5]. Over the past few decades, an unprecedented advance in genotyping technologies has led to a marked increase in the publication of genome-wide association studies (GWAS) [6]. GWAS results generally have much smaller P values than those of observational studies, which are expected to have higher numbers of false-positive noteworthy associations. However, in observational studies, the threshold P value is generally fixed at 0.05 and the small sample size of studies allows for a P value that is highly responsive to a change in the number of cases [5]. In the case of GWAS, the genome-wide significance threshold should be P<5×10-8 [7]. However, some uncertainty persists about the most appropriate genome-wide significance threshold. At the practical level, some initial GWAS used a threshold of P<1×10-7 [8-10]. The general rule, however, is that associations with P< 5×10-8 are considered replicable [11]. And, associations with P≥1×10-7 are not accepted unless proven by more stringent replication [5].

Discovering noteworthy variants

The common misunderstanding of the P value is that it is, in fact, not the probability of the null hypothesis being rejected by mistake but the probability of the null hypothesis. Therefore, the evaluation of the hypothesis requires a Bayesian approach that requires prior probability of the hypothesis and the data [12]. To date, 2 major Bayesian approaches in the assessment of false report probability were published, the false-positive report probability (FPRP) and the Bayesian false-discovery probability (BFDP) [12,13]. FPRP and BFDP have been used in various genetic studies and field synopses in cancer studies (i.e., lung, ovarian, colorectal, gastric, hematologic) to identify genuine noteworthy genetic variants [5,14-21]. However, attempts to discover noteworthy variants in autoimmune diseases using FPRP and BFDP are scarce.

1. False-positive report probability

FPRP is defined as “the probability of no true association between a gene variant and disease (null hypothesis)” for a statistically significant finding now assumed as a P<0.05 [11]. Developed by Wacholder et al. [12], FPRP is calculated with the observed P value, statistical power of the test, and the prior probability that an association is true. The prior probabilities we assumed when calculating FPRP were 10-3 for a candidate gene variant and 10-6 for a random single nucleotide polymorphism (SNP) as suggested by Wacholder et al. [12]. In our previous field synopsis of SLE [4], we calculated FPRP at those 2 assumed prior probabilities. The statistical power to detect an odds ratio (OR) of 1.2 and 1.5 was used for FPRP at both prior probabilities. Statistical power based on the ability to detect an OR of 1.5 (or its reciprocal 1/1.5=0.67 for an OR<1) was first proposed by Wacholder et al. [12], which we thought might be too conservative. Thus, we advocate using statistical power to detect an OR of the median among the results of studies and 1.5. The FPRP can be obtained using the following equation:

(1) FPRP=α(1-π)α(1-π)+(1-β)π

where π is the prior probability, α is the lowest level of significance at which a test is noteworthy (α=0.05), while (1-β) is the statistical power obtained using the following equation:

(2) 1-β= φ[log(ORA/ORO)]σ- Zα/2

where φ is the cumulative distribution function of the standard normal distribution and Zα/2 is the α/2 point of the standard cumulative normal distribution. For the actual computation of FPRP, σ and Zα/2 are replaced by the standard error of the logOR estimates and the 2-sided P value point of the standard normal distribution. All FPRP computations were performed using the Excel spreadsheet provided by Wacholder et al. [12], and associations with FPRP <0.2 were considered noteworthy as recommended by the authors.

2. Bayesian false-discovery probability

BFDP values can be obtained using methods created by Wakefield [13]. This provides information based on the cost of a false discovery and a false nondiscovery. Different from FPRP, BFDP is calculated using the following equation:

(3) BFDP=ABF×POABF×PO+1

where PO is the prior odds of the null hypothesis and is equal to πo/(1-πo) wherein πo is the prior probability of the null hypothesis and ABF is the approximate Bayesian factor computed using OR and standard error. Its approximation is based on a logistic regression model instead of a standard normal distribution. The noteworthiness is assessed with the cutoff value of 0.8 for BFDP, which means a false nondiscovery 4 times as costly as a false discovery [13].

BFDP seems more reasonable with sound methodological derivation than FPRP. While FPRP is stated as the lowest FPRP value at which a test would yield a noteworthy finding and assumes a specific point as a prior [12], BFDP uses average over all alternatives as a prior [13]. In other words, FPRP produces posterior null estimates that are smaller than those produced by BFDP because FPRP is essentially the lower bound on the posterior probability corresponding to the observed estimates [22]. All BFDP computations were performed using the Excel spreadsheet provided by Wakefield (http://faculty.washington/edu/jonno/cv.html) [13].

3. Tendencies of FPRP and BFDP with P values

The main purpose of the methods we introduced in this review is to discover false-positive results, which already satisfy the current scientific statistical standards regarding a P value indicating statistical significance. Therefore, with the published results of the SLE field synopsis and systematic review [4], we calculated the proportion of noteworthy variants relevant to the P value. A conventional meta-analysis of observational studies defines its significance with a P value of less than 0.05, whereas a meta-analysis of GWAS uses 5×10-8 as a threshold. We excluded data with which the results of FPRP or BFDP were not mathematically calculable, expressed as “NA.”

The ratio for the noteworthy variants out of positive findings in the meta-analysis of observational studies decreased stiffly as the P value exceeded 0.001 for both FPRP and BFDP (Fig. 1). In the same manner, the ratio of the noteworthy findings among the meta-analysis results of GWAS by FPRP computation decreased to 0.5 with a P value >10-5 (Fig. 2), while BFDP also showed a sudden decrease in the number of noteworthy variants at a P≥10-5. The difference between FPRP and BFDP is that more genetic variants located in the borderline (5×10-8 <P<0.05) significance in GWAS meta-analyses were noteworthy in BFDP than in FPRP (Fig. 2).

Fig. 1.

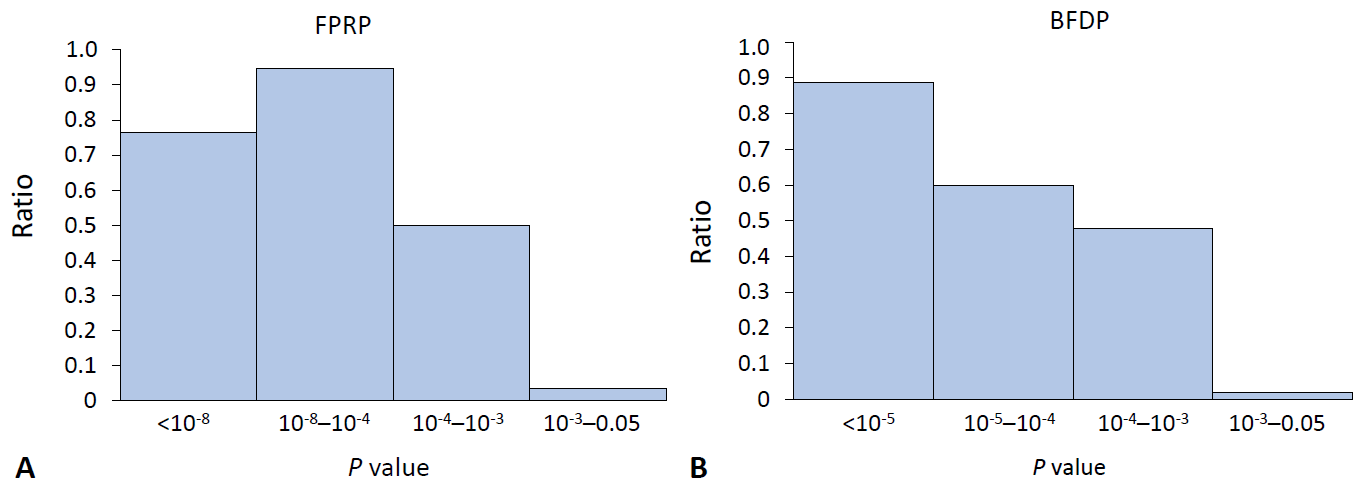
The ratio of noteworthy findings over statistically significant findings by FPRP and BFDP in the meta-analysis of observational studies. The y-axis is the ratio of noteworthy variants by FPRP (A): 0.76, 0.95, 0.5, 0.04 from left to right; and by BFDP (B): 0.89, 0.6, 0.48, 0.02. The x-axis is the range of P values. BFDP, Bayesian false-discovery probability; FPRP, false-positive report probability.

Fig. 2.

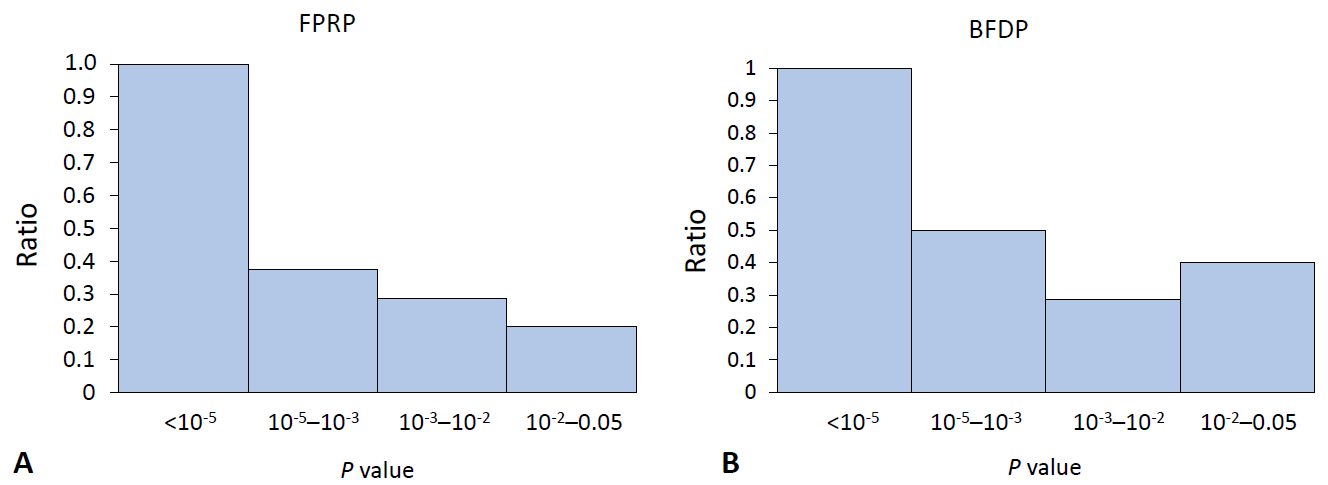
The ratio of noteworthy findings by FPRP and BFDP in the meta-analysis of genome-wide association studies. The y-axis is the ratio of noteworthy findings over statistically significant findings by FPRP (A): 1.0, 0.38, 0.29, 0.2; and by BFDP (B): 1.0, 0.5, 0.29, 0.4. BFDP, Bayesian false-discovery probability; FPRP, false-positive report probability.

The current cutoff for a P<0.05 might be too broad, as it would yield too many false-positive results, thus leading to the overinterpretation of the retrieved results. According to the findings of this review, the statistical significance in the meta-analysis of observational studies requires evaluation with a more stringent P value. Furthermore, GWAS meta-analysis results are highly reliable because all variants under a P value of 5×10-8 were noteworthy with FPRP and BFDP computations (Table 1).

Proportion of noteworthy gene variants by statistical approach and significance threshold

Noteworthy genetic variants in SLE and their functions

Our previous systematic review of SLE calculated noteworthiness of published significant genetic variants using FPRP and BFDP [4]. Table 1 summarizes the proportion of noteworthy gene variants in each type of GWAS according to the different statistical approaches and significance thresholds. Seventy-five distinct genes with 133 genotype comparisons from observational studies were identified as significant. Of the 133 genotype comparisons, 23 (17%) and 11 (8%) were verified as noteworthy (<0.2) using FPRP estimation at a prior probability of 10-3 and 10-6 with statistical power to detect an OR of 1.2. In addition, 34 (26%) and 18 (14%) showed a noteworthiness at a prior probability of 10-3 and 10-6 with a statistical power to detect an OR of 1.5. In terms of BFDP, 50 (38%) and 29 (22%) comparisons had noteworthy findings (<0.8) at a prior probability of 10-3 and 10-6. Seventy genes with 89 genotype comparisons extracted from GWAS were reportedly significant with a P<5×10-8. On FPRP, 64 comparisons were noteworthy (<0.2) at both prior probabilities of 10-3 and 10-6 with a statistical power to detect an OR of 1.2 and 1.5. The noteworthiness of 25 comparisons was not available for the same reason as mentioned above. With respect to BFDP estimations, all of the calculated values at both prior probabilities of 10-3 and 10-6 were <0.8, indicating noteworthiness. As a result, all of the statistically significant results of the meta-analyses of GWAS were assessed to be definitely noteworthy under FPRP and BFDP. A total of 25 genes with 27 genotype comparisons were organized, which had a borderline statistical significance (P value of 0.05 to 5×10-8). Under FPRP estimation, 13 (48%) and 2 (7%) were assessed to be noteworthy at a prior probability of 10-3 and 10-6 with a statistical power to detect an OR of 1.2. Moreover, 13 (48%) and 2 (7%) were identified as noteworthy at a prior probability of 10-3 and 10-6 with a statistical power to detect an OR of 1.5. In terms of BFDP, 15 (56%) and 1 (4%) comparisons were found noteworthy at a prior probability of 10-3 and 10-6.

We found that the GWAS meta-analysis results were highly reliable because all variants under a P value of 5×10-8 were evaluated as noteworthy with FPRP and BFDP computations. The GWAS results with P<5×10-8 could be identically replicated in observational studies. In addition, of the 27 genotype comparisons that had borderline statistical significance, 13 (48%) were noteworthy under both Bayesian methods, suggesting that results with a P value of 0.05 to 5×10-8 may be genuine associations. To verify the results obtained from genetic analyses, both Bayesian approaches may have advantages, especially for the interpretation of results obtained from observational studies. When determining the results of GWAS with P values ranging between 0.05 and 5×10-8, statistical approaches other than single standard significance may be beneficial, and we were able to confirm significance in almost half of the genetic variants within this borderline significance range. Therefore, it is attractive to speculate that genetic variants with borderline significance require further analysis for a genuine association [4].

Noteworthy genetic variants in SLE and their functions are summarized in Table 2. Investigation of the sorted list of significant genes identified a prominent representation of genes that have a role in interferon (IFN) signaling, which was in line with previous reports [23,24]. These genes were IFIH1, IRF5, IRF8, and STAT4 from the observational studies and IFIH1, IRF5, IRF7, IRF8, PRDM1-ATG5, STAT4, ad TYK2 from GWAS. IFN-α, a type I IFN, is traditionally known to be concerned with a defense against viruses and its involvement in breaking self-tolerance via the activation of antigen-presenting cells after absorbing self-materials [25], which explains some essential parts of the current understanding of SLE [26]. In addition, the proportion of genes whose function is related to nuclear factor kappa B (NF-κB) signaling was also outstanding. NF-κB plays a critical role in proinflammatory processes through regulating the expression of tumor necrosis factor-α (TNF-α), toll-like receptors, and interleukin 1 receptor [27]. These were MECP2 and TNFAIP3 from observational studies and IKBKE, IRAK1, MECP2, SLC15A4, TNFAIP3, TNIP1, and UBE2L3 from GWAS. Other genes with relevance to the immune system such as complement activation, apoptosis, and neutrophil, monocyte, NK cell, and B- and T-cell signaling were significantly related to the genetic susceptibility loci for SLE [28].

Noteworthy genetic variants and their functions

Gene network analysis

As the bioinformatic open resources are overwhelming, we thought that using noteworthy genetic variants for gene network analyses with open source methods should derive a genuine etiopathology of the respective disease. Several databases have compiled data from experimental and computational sources, integrating extensive protein-protein interactions (PPIs) or gene-gene interactions. STRING (Search Tool for the Retrieval of Interacting Genes/Proteins) and GeneMANIA are representative freely available databases that were constructed from various biological and literature sources. The utilization of these interactions among genes aids the understanding of the underlying biological mechanisms as well as the hidden pathology of human disease associated with the genes [29]. Since different databases are constructed based on different biological evidence, the utilization of the appropriate network database is very critical for identifying meaningful interaction information. A recent interesting benchmarking study comparing the performance of different network databases in the context of virus-host interactions and STRING databases revealed overall good performance for detecting known host factors for various human genes [30]. In this review, we introduced the process of sorting out noteworthy variants from the known statistically significant variants; furthermore, we applied the 2 representative databases STRING and GeneMANIA and genetic variants associated with SLE in our previous field synopsis [4] to the STRING database to construct a PPI network.

1. GeneMANIA

The GeneMANIA database [31] includes 1,800 networks covering 500 million gene-gene interactions and PPI from 9 organisms (Arabidopsis thaliana, Caenorhabditis elegans, Danio rerio, Drosophila melanogaster, Escherichia coli, Homo sapiens, Mus musculus, Rattus norvegicus, and Saccharomyces cerevisiae). It provides a comprehensive compiled network from hundreds of different sources such as coexpression, genetic interactions, colocalization information, and shared protein domains. GeneMANIA utilizes linear regression models to combine different functional association networks from multiple data sources and Gaussian field label propagation methods are applied to predict the gene function based on composite functional networks. The combined edge scores are calculated as the weighted sum of scores by emphasizing the directly connected genes.

2. STRING database

The STRING 9.1 network database [32] is one of the largest databases of direct (physical) PPI and indirect (functional) interactions constructed from various data sources. The STRING database covers 9.6 million proteins from 2,031 different organisms and incorporates PPI information from a number of known databases, such as Reactome, KEGG pathways, HPRD, BioGrid, and MINT as well as automated text mining including PubMed abstracts and OMIM database. It also includes computationally predicted PPI by utilizing ortholog information between different species. The STRING database provides the PPI score using a naïve Bayesian algorithm to combine different scores from different biological evidence with a correction for random observation probability of interactions. Thus, the combined STRING edge score is used to indicate strong confidence for such PPI.

3. Construction of PPI networks using the STRING database

In our study, we used the STRING database to identify the PPI associated with gene mapping to genetic variants of SLE. First, our gene lists represented by gene symbol were converted to Ensembl protein identifiers using mapping information from the NCBI ftp server. Some of the gene symbols were preprocessed for conversion to official gene symbols before Ensembl ID mapping due to their ambiguity. Based on given Ensembl protein identifiers and the minimum PPI score, each PPI is extracted from the STRING databases. Depending on interests, we also extracted the closely associated genes with current gene lists using the Random Walk with Restart Algorithm [33], where functional closeness of 2 gene lists is represented by an XD score using the STRING database. We applied our in-house program written with Perl and C. Once the functionally related genes are selected, Cytoscape [34], which is a free software package for visualizing, modeling, and analyzing molecular and genetic interaction networks, is used for network visualization. To import the PPI file into Cytoscape, users must prepare the network input file constructed from at least 3 columns: source node, interaction type, and target node. Edge attributes such as interaction score can also be imported into the network. The node property file can be prepared to indicate any property of each gene/proteins such as name, function, and node type (i.e., node data source). These 2 files (i.e., network file, node property file) were imported into Cytoscape for the visualization.

4. PPI network for SLE

Here we constructed the PPI network with genes mapping to the compiled reported genetic variants of SLE. Fig. 3A represents the PPI networks with genes having genetic variants with statistical significance from observational studies. Among the 135 genetic variants mapping to 79 genes, 54 genes revealed 846 interactions between them and IL-6, TP53, IL-10, ITGAM, and NFKB1 were identified as strong hub nodes. In addition, TRAF6, IRF5, ITGAM, TNFAIP3, and BLK were identified as critical genes having more than 4 reported genetic variants in SLE, which shows a strong association of such genes with SLE. Fig. 3B and 3C also show the PPI networks with statistically significant and borderline genes from GWAS studies (i.e., P<5×10-8, 5×10-8 <P<0.05), respectively. TNFSF4, CD44, STAT4, and TNAFAIP2 also showed a strong association with SLE from GWAS studies. Moreover, PTPRC, STAT4, and IL-10 also revealed strong hubness in the PPI network.

Fig. 3.

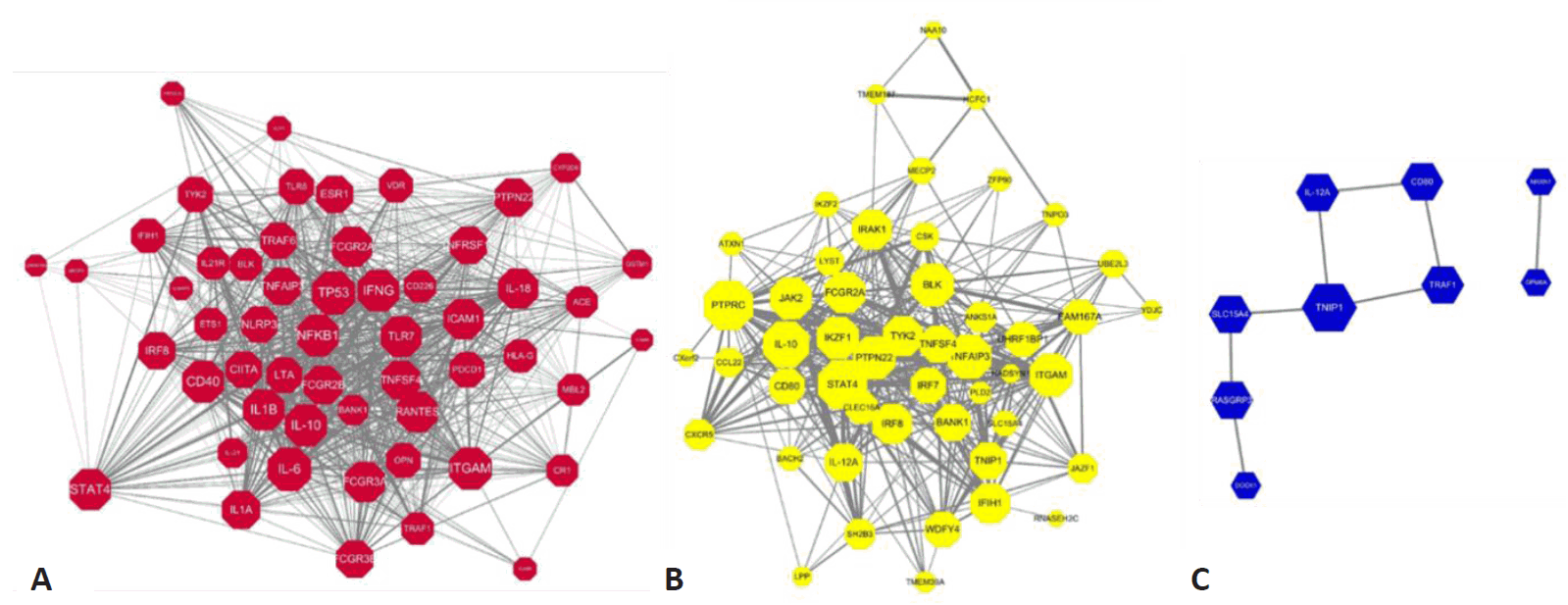
PPI network with genes mapping to the statistically significant genetic variants. (A) Statistically significant genes from observational studies (T1: P<0.05), (B) statistically significant genes (T2: P<5×10-8) from GWAS, (C) statistically significant genes at the borderline (T3: 5×10-8<P<0.05) from GWAS. Node size represents the number of interactions, while edge width represents the PPI score from the STRING (Search Tool for the Retrieval of Interacting Genes/Proteins) databases. The width of interactions shows the strength of the interactions mapping to the STRING score. PPI, protein-protein interactions; GWAS, gene-wide association studies.

Next, we integrated these PPI networks with the genes mapping to overall genetic variants of SLE from 3 criteria. As shown in Fig. 4, genes from observational studies, GWAS with 2 different P values, are closely connected within the PPI network. Many genes have genetic variants identified from at least 2 studies (i.e., orange, green, and purple nodes). Among the 148 genes, 97 revealed 1,554 PPI. Interestingly, TP53, PTPRC, NFKB1, IL-6, IL-10, and STAT4 have more than 60 interactions in the PPI network and IL-10, STAT4, ITGAM, FCGR2A, and PTPN22 are also identified as genes having genetic variants in SLE from both observational and GWAS.

Fig. 4.

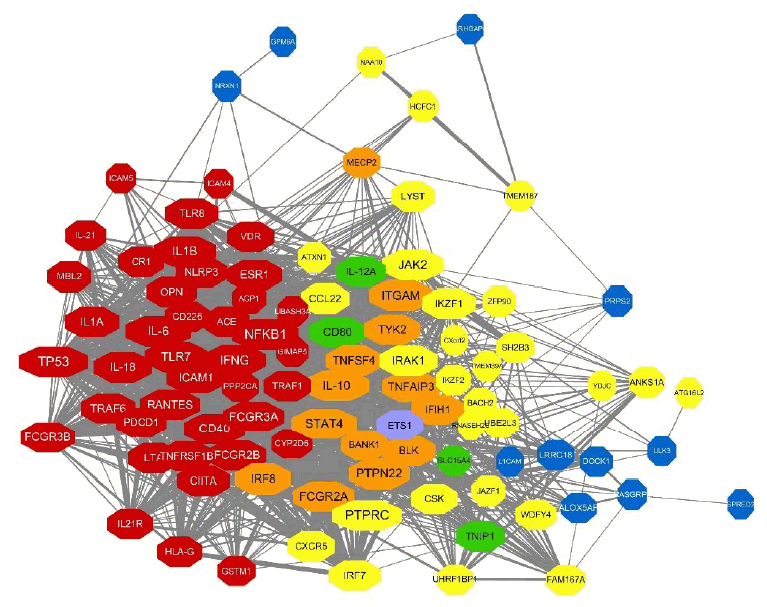
Compiled PPI network with genes mapping to the genetic variants identified using different criteria. The node color of genes represents the evidence for genetic variants mapping to genes. Red indicates genes from observational studies (T1), yellow indicates statistically significant genes from GWAS (T2), and blue indicates borderline significant genes from GWAS (T3). Orange, green, and purple genes are genetic variants of SLE identified from at least 2 criteria (T1 and T2, T2 and T3, and T1 and T3, respectively). Note that miR-146a is identified from all 3 criteria (T1, T2, and T3) but not shown in the PPI network. PPI, protein-protein interaction; GWAS, genome-wide association study.

Discussion

In this review, we provided general concepts for applying Bayesian methods and gene network analyses to interpret genetic epidemiology results. The Bayesian approach is unfamiliar in genetics and the need for filtering true-positive or “noteworthy” genetic variants is unavoidable due to the enlarging amount of research data. Although a meta-analysis provides one of the highest levels of evidence within research in the medical field, different meta-analyses from different groups must be integrated and rehighlighted. We refined scattered positive data of meta-analyses in SLE with discovering false-positive results using Bayesian approaches, FPRP and BFDP, consequently suggesting a comprehensive PPI for the disease.

The Bayesian approach and its value depend on the prior probabilities, the calculation of power (1-β), and the probability of type I error (α). FPRP has been criticized for its heuristic derivation of α and 1-β as P0(t) and Pδ(t), for which P0(t) is the probability of observing a value greater than |t| or less than -|t| under the null hypothesis, versus Pδ(t) under the alternative; in other words, α and 1-β are pre-study quantities as properties of a test, while P0(t) and Pδ(t) are post-study parameters [22], in fact, not related to the test genuine parameters. Also, FPRP calculates its likelihood with its tail-area; thus, information is lost compared to BFDP, in which the exact ratio of the probability densities in the indicated point is calculated. Still, both assessments are recommended in a study to determine the true impact of the discovery.

Our gene network construction with genes having noteworthy genetic variants found sound PPI in SLE. The hub genes with more than 50 interactions were PTPRC, TP53, NFKB1, IL6, STAT4, IL10, ITGAM, TLR7, IFNG, IL1B, FCGR2A, JAK2, CD40, FCGR3A, PTPN22, RANTES, ICAM1, IRAK1, FCGR2B, CD80, IL18, and TNFAIP3.

The PPI construction using the STRING database provides insight for further wet lab-based research. On the other hand, although observational studies or GWAS elicited statistically significant genetic variations, they might not reveal the actual biological mechanism until epigenetic or molecular changes are proven. To overcome this hurdle, a combination analysis of gene expression and the matching SNP profile may be the way forward for discovering the disease etiology.

Notes

No potential conflict of interest relevant to this article was reported.

Acknowledgements

This study was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2017R1D1A1B03032457) and Hankuk University of Foreign Studies Research Fund.

References

1. Ioannidis JP. The mass production of redundant, misleading, and conflicted systematic reviews and meta-analyses. Milbank Q 2016;94:485–514.
2. Pan Z, Trikalinos TA, Kavvoura FK, Lau J, Ioannidis JP. Local literature bias in genetic epidemiology: an empirical evaluation of the Chinese literature. PLoS Med 2005;2e334.
3. Park JH, Eisenhut M, van der Vliet HJ, Shin JI. Statistical controversies in clinical research: overlap and errors in the meta-analyses of microRNA genetic association studies in cancers. Ann Oncol 2017;28:1169–82.
4. Jeong DY, Lee SW, Park YH, Choi JH, Kwon YW, Moon G, et al. Genetic variation and systemic lupus erythematosus: A field synopsis and systematic meta-analysis. Autoimmun Rev 2018;17:553–66.
5. Park JH, Geum DI, Eisenhut M, van der Vliet HJ, Shin JI. Bayesian statistical methods in genetic association studies: Empirical examination of statistically non-significant Genome Wide Association Study (GWAS) meta-analyses in cancers: A systematic review. Gene 2019;685:170–8.
6. McCarthy MI, Abecasis GR, Cardon LR, Goldstein DB, Little J, Ioannidis JP, et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet 2008;9:356–69.
7. Panagiotou OA, Ioannidis JP, Genome-Wide Significance P. What should the genome-wide significance threshold be? Empirical replication of borderline genetic associations. Int J Epidemiol 2012;41:273–86.
8. Maraganore DM, de Andrade M, Lesnick TG, Strain KJ, Farrer MJ, Rocca WA, et al. High-resolution whole-genome association study of Parkinson disease. Am J Hum Genet 2005;77:685–93.
9. Stacey SN, Manolescu A, Sulem P, Rafnar T, Gudmundsson J, Gudjonsson SA, et al. Common variants on chromosomes 2q35 and 16q12 confer susceptibility to estrogen receptor-positive breast cancer. Nat Genet 2007;39:865–9.
10. Zanke BW, Greenwood CM, Rangrej J, Kustra R, Tenesa A, Farrington SM, et al. Genome-wide association scan identifies a colorectal cancer susceptibility locus on chromosome 8q24. Nat Genet 2007;39:989–94.
11. Hoggart CJ, Clark TG, De Iorio M, Whittaker JC, Balding DJ. Genomewide significance for dense SNP and resequencing data. Genet Epidemiol 2008;32:179–85.
12. Wacholder S, Chanock S, Garcia-Closas M, El Ghormli L, Rothman N. Assessing the probability that a positive report is false: an approach for molecular epidemiology studies. J Natl Cancer Inst 2004;96:434–42.
13. Wakefield J. A Bayesian measure of the probability of false discovery in genetic epidemiology studies. Am J Hum Genet 2007;81:208–27.
14. Barrdahl M, Rudolph A, Hopper JL, Southey MC, Broeks A, Fasching PA, et al. Gene-environment interactions involving functional variants:Results from the Breast Cancer Association Consortium. Int J Cancer 2017;141:1830–40.
15. Braem MG, Schouten LJ, Peeters PH, van den Brandt PA, Onland-Moret NC. Genetic susceptibility to sporadic ovarian cancer: a systematic review. Biochim Biophys Acta 2011;1816:132–46.
16. Dong LM, Potter JD, White E, Ulrich CM, Cardon LR, Peters U. Genetic susceptibility to cancer: the role of polymorphisms in candidate genes. JAMA 2008;299:2423–36.
17. Engels EA, Wu X, Gu J, Dong Q, Liu J, Spitz MR. Systematic evaluation of genetic variants in the inflammation pathway and risk of lung cancer. Cancer Res 2007;67:6520–7.
18. Montazeri Z, Theodoratou E, Nyiraneza C, Timofeeva M, Chen W, Svinti V, et al. Systematic meta-analyses and field synopsis of genetic association studies in colorectal adenomas. Int J Epidemiol 2016;45:186–205.
19. Pathak A, Wenzlaff AS, Hyland PL, Cote ML, Keele GR, Land S, et al. Apoptosis-related single nucleotide polymorphisms and the risk of non-small cell lung cancer in women. J Cancer Ther Res 2014;310.7243/2049-7962-3-1.
20. Theodoratou E, Montazeri Z, Hawken S, Allum GC, Gong J, Tait V, et al. Systematic meta-analyses and field synopsis of genetic association studies in colorectal cancer. J Natl Cancer Inst 2012;104:1433–57.
21. Vijayakrishnan J, Houlston RS. Candidate gene association studies and risk of childhood acute lymphoblastic leukemia: a systematic review and meta-analysis. Haematologica 2010;95:1405–14.
22. Lucke JF. A critique of the false-positive report probability. Genet Epidemiol 2009;33:145–50.
23. Crow MK. Advances in understanding the role of type I interferons in systemic lupus erythematosus. Curr Opin Rheumatol 2014;26:467–74.
24. Ghodke-Puranik Y, Niewold TB. Genetics of the type I interferon pathway in systemic lupus erythematosus. Int J Clin Rheumtol 2013;8
25. Blanco P, Palucka AK, Gill M, Pascual V, Banchereau J. Induction of dendritic cell differentiation by IFN-alpha in systemic lupus erythematosus. Science 2001;294:1540–3.
26. Interferon alpha as a primary pathogenic factor in human lupus. J Interferon Cytokine Res 2011;31:887–92.
27. Beyaert R, Heyninck K, Van Huffel S. A20 and A20-binding proteins as cellular inhibitors of nuclear factor-kappa B-dependent gene expression and apoptosis. Biochem Pharmacol 2000;60:1143–51.
28. Ghodke-Puranik Y, Niewold TB. Immunogenetics of systemic lupus erythematosus: A comprehensive review. J Autoimmun 2015;64:125–36.
29. Sevimoglu T, Arga KY. The role of protein interaction networks in systems biomedicine. Comput Struct Biotechnol J 2014;11:22–7.
30. Taye B, Vaz C, Tanavde V, Kuznetsov VA, Eisenhaber F, Sugrue RJ, et al. Benchmarking selected computational gene network growing tools in context of virus-host interactions. Sci Rep 2017;7:5805.
31. Warde-Farley D, Donaldson SL, Comes O, Zuberi K, Badrawi R, Chao P, et al. The GeneMANIA prediction server: biological network integration for gene prioritization and predicting gene function. Nucleic Acids Res 2010;38:W214–20.
32. Franceschini A, Szklarczyk D, Frankild S, Kuhn M, Simonovic M, Roth A, et al. STRING v9.1: protein-protein interaction networks, with increased coverage and integration. Nucleic Acids Res 2013;41:D808–15.
33. Ko Y, Cho M, Lee JS, Kim J. Identification of disease comorbidity through hidden molecular mechanisms. Sci Rep 2016;6:39433.
34. Cline MS, Smoot M, Cerami E, Kuchinsky A, Landys N, Workman C, et al. Integration of biological networks and gene expression data using Cytoscape. Nat Protoc 2007;2:2366–82.
35. Bentham J, Morris DL, Graham DSC, Pinder CL, Tombleson P, Behrens TW, et al. Genetic association analyses implicate aberrant regulation of innate and adaptive immunity genes in the pathogenesis of systemic lupus erythematosus. Nat Genet 2015;47:1457–64.
36. Oparina NY, Delgado-Vega AM, Martinez-Bueno M, Magro-Checa C, Fernandez C, Castro RO, et al. PXK locus in systemic lupus erythematosus: fine mapping and functional analysis reveals novel susceptibility gene ABHD6. Ann Rheum Dis 2015;74e14.
37. Vaughn SE, Foley C, Lu X, Patel ZH, Zoller EE, Magnusen AF, et al. Lupus risk variants in the PXK locus alter B-cell receptor internalization. Front Genet 2014;5:450.
38. National Center for Biotechnology Information. RefSeq: NCBI Reference Sequence Database [Internet]. Bethesda (MD): National Center for Biotechnology Information; [cited 2020 April 9]. Available from: https://www.ncbi.nlm.nih.gov/refseq/.
39. Lessard CJ, Sajuthi S, Zhao J, Kim K, Ice JA, Li H, et al. Identification of a systemic lupus erythematosus risk locus spanning ATG16L2, FCHSD2, and P2RY2 in Koreans. Arthritis Rheumatol 2016;68:1197–209.
40. Zhang Y, Yang J, Zhang J, Sun L, Hirankarn N, Pan HF, et al. Genomewide search followed by replication reveals genetic interaction of CD80 and ALOX5AP associated with systemic lupus erythematosus in Asian populations. Ann Rheum Dis 2016;75:891–8.
41. Molineros JE, Yang W, Zhou XJ, Sun C, Okada Y, Zhang H, et al. Confirmation of five novel susceptibility loci for systemic lupus erythematosus (SLE) and integrated network analysis of 82 SLE susceptibility loci. Hum Mol Genet 2017;26:1205–16.
42. Morris DL, Sheng Y, Zhang Y, Wang YF, Zhu Z, Tombleson P, et al. Genome-wide association meta-analysis in Chinese and European individuals identifies ten new loci associated with systemic lupus erythematosus. Nat Genet 2016;48:940–6.
43. Bergeron D. Identification et caractérisation d'une deuxième protéine codée par le gène ATXN1 Sherbrooke (CA): Université de Sherbrooke; 2013.
44. Oyake T, Itoh K, Motohashi H, Hayashi N, Hoshino H, Nishizawa M, et al. Bach proteins belong to a novel family of BTB-basic leucine zipper transcription factors that interact with MafK and regulate transcription through the NF-E2 site. Mol Cell Biol 1996;16:6083–95.
45. Vahedi G, Kanno Y, Furumoto Y, Jiang K, Parker SC, Erdos MR, et al. Super-enhancers delineate disease-associated regulatory nodes in T cells. Nature 2015;520:558–62.
46. Yokoyama K, Su Ih, Tezuka T, Yasuda T, Mikoshiba K, Tarakhovsky A, et al. BANK regulates BCR-induced calcium mobilization by promoting tyrosine phosphorylation of IP3 receptor. EMBO J 2002;21:83–92.
47. Lee YH, Bae SC, Choi SJ, Ji JD, Song GG. Genome-wide pathway analysis of genome-wide association studies on systemic lupus erythematosus and rheumatoid arthritis. Mol Biol Rep 2012;39:10627–35.
48. Lee YH, Bae SC, Choi SJ, Ji JD, Song GG. Associations between the functional CD40 rs4810485 G/T polymorphism and susceptibility to rheumatoid arthritis and systemic lupus erythematosus: a meta-analysis. Lupus 2015;24:1177–83.
49. Lessard CJ, Adrianto I, Kelly JA, Kaufman KM, Grundahl KM, Adler A, et al. Identification of a systemic lupus erythematosus susceptibility locus at 11p13 between PDHX and CD44 in a multiethnic study. Am J Hum Genet 2011;88:83–91.
50. Sheng YJ, Xu JH, Wu YG, Zuo XB, Gao JP, Lin Y, et al. Association analyses confirm five susceptibility loci for systemic lupus erythematosus in the Han Chinese population. Arthritis Res Ther 2015;17:85.
51. Shojaa M, Aghaie M, Qorbani M, Khashayar P, Amoli M, Keshtkar AA, et al. Association of the CTLA-4 1722TC polymorphism and systemic lupus erythematosus: a systematic review and meta analysis. Med J Islam Repub Iran 2014;28:132.
52. Zhang J, Zhang Y, Yang J, Zhang L, Sun L, Pan HF, et al. Three SNPs in chromosome 11q23.3 are independently associated with systemic lupus erythematosus in Asians. Hum Mol Genet 2014;23:524–33.
53. Odhams CA, Roberts AL, Vester SK, Duarte CST, Beales CT, Clarke AJ, et al. Interferon inducible X-linked gene CXorf21 may contribute to sexual dimorphism in Systemic Lupus Erythematosus. Nat Commun 2019;10:2164.
54. Wang C, Ahlford A, Jarvinen TM, Nordmark G, Eloranta ML, Gunnarsson I, et al. Genes identified in Asian SLE GWASs are also associated with SLE in Caucasian populations. Eur J Hum Genet 2013;21:994–9.
55. Yang W, Shen N, Ye DQ, Liu Q, Zhang Y, Qian XX, et al. Genome-wide association study in Asian populations identifies variants in ETS1 and WDFY4 associated with systemic lupus erythematosus. PLoS Genet 2010;6e1000841.
56. Zhu XW, Wang Y, Wei YH, Zhao PP, Wang XB, Rong JJ, et al. Comprehensive assessment of the association between FCGRs polymorphisms and the risk of systemic lupus erythematosus: evidence from a meta-analysis. Sci Rep 2016;6:31617.
57. Zhang Y, Zhang J, Yang J, Wang Y, Zhang L, Zuo X, et al. Meta-analysis of GWAS on two Chinese populations followed by replication identifies novel genetic variants on the X chromosome associated with systemic lupus erythematosus. Hum Mol Genet 2015;24:274–84.
58. Niu Z, Zhang P, Tong Y. Value of HLA-DR genotype in systemic lupus erythematosus and lupus nephritis: a meta-analysis. Int J Rheum Dis 2015;18:17–28.
59. Castano-Rodriguez N, Diaz-Gallo LM, Pineda-Tamayo R, Rojas-Villarraga A, Anaya JM. Meta-analysis of HLA-DRB1 and HLA-DQB1 polymorphisms in Latin American patients with systemic lupus erythematosus. Autoimmun Rev 2008;7:322–30.
60. Lee YH, Bae SC, Song GG. Meta-analysis of associations between functional HLA-G polymorphisms and susceptibility to systemic lupus erythematosus and rheumatoid arthritis. Rheumatol Int 2015;35:953–61.
61. Paul P, Rouas-Freiss N, Khalil-Daher I, Moreau P, Riteau B, Le Gal FA, et al. HLA-G expression in melanoma: a way for tumor cells to escape from immunosurveillance. Proc Natl Acad Sci U S A 1998;95:4510–5.
62. Kim K, Brown EE, Choi CB, Alarcon-Riquelme ME, Kelly JA, et al. Variation in the ICAM1-ICAM4-ICAM5 locus is associated with systemic lupus erythematosus susceptibility in multiple ancestries. Ann Rheum Dis 2012;71:1809–14.
63. J de AS, C A, P SG, S C. Systemic lupus erythematosus: old and new susceptibility genes versus clinical manifestations. Curr Genomics 2014;15:52–65.
64. Qi JH, Qi J, Xiang LN, Nie G. Association between IL-21 polymorphism and systemic lupus erythematosus: a meta-analysis. Genet Mol Res 2015;14:9595–603.
65. Webb R, Merrill JT, Kelly JA, Sestak A, Kaufman KM, Langefeld CD, et al. A polymorphism within IL21R confers risk for systemic lupus erythematosus. Arthritis Rheum 2009;60:2402–7.
66. Katkam SK, Rajasekhar L, Kumaraswami K, Kutala VK. Association of IL -6 -174 G>C polymorphism with the risk of SLE among south Indians: evidence from case-control study and meta-analysis. Lupus 2017;26:1491–501.
67. Chang Y, Sheng Y, Cheng Y, Lin Y, Zhu Z, Wen L, et al. Downregulated expression of LBH mRNA in peripheral blood mononuclear cells from patients with systemic lupus erythematosus. J Dermatol 2016;43:99–102.
68. Flesher DL, Sun X, Behrens TW, Graham RR, Criswell LA. Recent advances in the genetics of systemic lupus erythematosus. Expert Rev Clin Immunol 2010;6:461–79.
69. Lee YH, Lee HS, Choi SJ, Ji JD, Song GG. The association between the mannose-binding lectin codon 54 polymorphism and systemic lupus erythematosus: a meta-analysis update. Mol Biol Rep 2012;39:5569–74.
70. Webb R, Wren JD, Jeffries M, Kelly JA, Kaufman KM, Tang Y, et al. Variants within MECP2, a key transcription regulator, are associated with increased susceptibility to lupus and differential gene expression in patients with systemic lupus erythematosus. Arthritis Rheum 2009;60:1076–84.
71. Tang ZM, Wang P, Chang PP, Hasahya T, Xing H, Wang JP, et al. Association between rs2431697 T allele on 5q33.3 and systemic lupus erythematosus: case-control study and meta-analysis. Clin Rheumatol 2015;34:1893–902.
72. Lee YH, Song GG. Correlation between circulating osteopontin level in systemic lupus erythematosus and disease activity and associations between osteopontin polymorphisms and disease susceptibility: a meta-analysis. Lupus 2017;26:132–8.
73. Tan W, Sunahori K, Zhao J, Deng Y, Kaufman KM, Kelly JA, et al. Association of PPP2CA polymorphisms with systemic lupus erythematosus susceptibility in multiple ethnic groups. Arthritis Rheum 2011;63:2755–63.
74. Ramos PS, Criswell LA, Moser KL, Comeau ME, Williams AH, Pajewski NM, et al. A comprehensive analysis of shared loci between systemic lupus erythematosus (SLE) and sixteen autoimmune diseases reveals limited genetic overlap. PLoS Genet 2011;7e1002406.
75. Li Y, He X, Schembri-King J, Jakes S, Hayashi J. Cloning and characterization of human Lnk, an adaptor protein with pleckstrin homology and Src homology 2 domains that can inhibit T cell activation. J Immunol 2000;164:5199–206.
76. Daniel H, Kottra G. The proton oligopeptide cotransporter family SLC15 in physiology and pharmacology. Pflugers Arch 2004;447:610–8.
77. Kobayashi T, Shimabukuro-Demoto S, Yoshida-Sugitani R, Furuyama-Tanaka K, Karyu H, Sugiura Y, et al. The histidine transporter SLC15A4 coordinates mTOR-dependent inflammatory responses and pathogenic antibody production. Immunity 2014;41:375–88.
78. Lee YH, Choi SJ, Ji JD, Song GG. Association between toll-like receptor polymorphisms and systemic lupus erythematosus: a meta-analysis update. Lupus 2016;25:593–601.
79. Lessard CJ, Adrianto I, Ice JA, Wiley GB, Kelly JA, Glenn SB, et al. Identification of IRF8, TMEM39A, and IKZF3-ZPBP2 as susceptibility loci for systemic lupus erythematosus in a large-scale multiracial replication study. Am J Hum Genet 2012;90:648–60.
80. Bates JS, Lessard CJ, Leon JM, Nguyen T, Battiest LJ, Rodgers J, et al. Meta-analysis and imputation identifies a 109 kb risk haplotype spanning TNFAIP3 associated with lupus nephritis and hematologic manifestations. Genes Immun 2009;10:470–7.
81. Zhang MY, Yang XK, Pan HF, Ye DQ. Associations between TNFAIP3 gene polymorphisms and systemic lupus erythematosus risk: an updated meta-analysis. HLA 2016;88:245–52.
82. Yang ZC, Xu F, Tang M, Xiong X. Association between TNF-alpha promoter -308 A/G polymorphism and systemic lupus erythematosus susceptibility: a case-control study and meta-analysis. Scand J Immunol 2017;85:197–210.
83. Kataoka N, Bachorik JL, Dreyfuss G. Transportin-SR, a nuclear import receptor for SR proteins. J Cell Biol 1999;145:1145–52.
84. Kurreeman FA, Goulielmos GN, Alizadeh BZ, Rueda B, Houwing-Duistermaat J, Sanchez E, et al. The TRAF1-C5 region on chromosome 9q33 is associated with multiple autoimmune diseases. Ann Rheum Dis 2010;69:696–9.
85. Ge M, Yu W, Shi J, Zhang J, Wang M, Feng S, et al. TRAF1/C5 rs10818488 polymorphism is not a genetic risk factor for acquired aplastic anemia in a Chinese population. Hum Immunol 2015;76:19–21.
86. Namjou B, Choi CB, Harley IT, Alarcon-Riquelme ME, Network B, Kelly JA, et al. Evaluation of TRAF6 in a large multiancestral lupus cohort. Arthritis Rheum 2012;64:1960–9.
87. Diaz-Gallo LM, Sanchez E, Ortego-Centeno N, Sabio JM, Garcia-Hernandez FJ, de Ramon E, et al. Evidence of new risk genetic factor to systemic lupus erythematosus: the UBASH3A gene. PLoS One 2013;8e60646.
88. Parmar AS, Lappalainen M, Paavola-Sakki P, Halme L, Farkkila M, Turunen U, et al. Association of celiac disease genes with inflammatory bowel disease in Finnish and Swedish patients. Genes Immun 2012;13:474–80.
89. Maloverjan A, Piirsoo M, Michelson P, Kogerman P, Osterlund T. Identification of a novel serine/threonine kinase ULK3 as a positive regulator of Hedgehog pathway. Exp Cell Res 2010;316:627–37.
90. Zhou TB, Jiang ZP, Lin ZJ, Su N. Association of vitamin D receptor gene polymorphism with the risk of systemic lupus erythematosus. J Recept Signal Transduct Res 2015;35:8–14.
91. Zhang Y, Wang YF, Yang J, Zhang J, Sun L, Hirankarn N, et al. Meta-analysis of two Chinese populations identifies an autoimmune disease risk allele in 22q11.21 as associated with systemic lupus erythematosus. Arthritis Res Ther 2015;17:67.

Article information Continued

Copyright © 2021 by The Korean Pediatric Society

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Fig. 1.

Fig. 1.

The ratio of noteworthy findings over statistically significant findings by FPRP and BFDP in the meta-analysis of observational studies. The y-axis is the ratio of noteworthy variants by FPRP (A): 0.76, 0.95, 0.5, 0.04 from left to right; and by BFDP (B): 0.89, 0.6, 0.48, 0.02. The x-axis is the range of P values. BFDP, Bayesian false-discovery probability; FPRP, false-positive report probability.

Fig. 2.

Fig. 2.

The ratio of noteworthy findings by FPRP and BFDP in the meta-analysis of genome-wide association studies. The y-axis is the ratio of noteworthy findings over statistically significant findings by FPRP (A): 1.0, 0.38, 0.29, 0.2; and by BFDP (B): 1.0, 0.5, 0.29, 0.4. BFDP, Bayesian false-discovery probability; FPRP, false-positive report probability.

Fig. 3.

Fig. 3.

PPI network with genes mapping to the statistically significant genetic variants. (A) Statistically significant genes from observational studies (T1: P<0.05), (B) statistically significant genes (T2: P<5×10-8) from GWAS, (C) statistically significant genes at the borderline (T3: 5×10-8<P<0.05) from GWAS. Node size represents the number of interactions, while edge width represents the PPI score from the STRING (Search Tool for the Retrieval of Interacting Genes/Proteins) databases. The width of interactions shows the strength of the interactions mapping to the STRING score. PPI, protein-protein interactions; GWAS, gene-wide association studies.

Fig. 4.

Fig. 4.

Compiled PPI network with genes mapping to the genetic variants identified using different criteria. The node color of genes represents the evidence for genetic variants mapping to genes. Red indicates genes from observational studies (T1), yellow indicates statistically significant genes from GWAS (T2), and blue indicates borderline significant genes from GWAS (T3). Orange, green, and purple genes are genetic variants of SLE identified from at least 2 criteria (T1 and T2, T2 and T3, and T1 and T3, respectively). Note that miR-146a is identified from all 3 criteria (T1, T2, and T3) but not shown in the PPI network. PPI, protein-protein interaction; GWAS, genome-wide association study.

Table 1.

Proportion of noteworthy gene variants by statistical approach and significance threshold

Meta-analyses No. of SNP studies P<0.05 FPRP values at prior probability
 BFDP 0.001 BFDP 0.000001
OR 1.2
 OR 1.5
0.001 0.000001 0.001 0.000001
Observational studies 133 133 (100) 23 (17) 11 (8) 34 (26) 18 (14) 50 (38) 29 (22)
GWAS (P<5×10-8)a) 89 89 (100) 64 (100) 64 (100) 64 (100) 64 (100) 89 (100) 89 (100)
GWAS (5×10-8<P<0.05) 27 27 (100) 13 (48) 2 (7) 13 (48) 2 (7) 15 (56) 1 (4)

Values are presented as number (%).

SNP, single nucleotide polymorphism; FPRP, false-positive report probability; OR, odds ratio; BFDP, Bayesian false-discovery probability; GWAS, genome-wide association studies.

a)

The noteworthiness of 25 comparisons was not available for FPRP among 89 genotype comparisons extracted from meta-analyses of GWAS with a P<5×10-8.

Table 2.

Noteworthy genetic variants and their functions

Study Gene Variant (RS number) Ethnicity, study No. (types of study) Comparison OR (95% CI) P value Function of genes
Bentham, et al. 2015 [35] ABHD6-PXK rs9311676 European 2 (MG) C<T 1.17 (1.13–1.22) 3.06×10-14 ABHD6 gene codes for the abhydrolase domain-containing protein 6. ABHD6 catalyzes the hydrolysis of 2-arachidonylglycerol and takes part in the endocannabinoid signaling regulation. [36] PXK gene encodes a phox (PX) domain-containing protein which may be involved in synaptic transmission and the ligand-induced internalization and degradation of epidermal growth factors. PXK also operates on the B-cell antigen receptor (BCR) and influences the rate of BCR internalization. [37,38]
Lessard, et al. 2016 [39] AHNAK2 rs1048257 Chinese 2 (MG) T<C 0.82 (0.76–0.89) 8.66×10-7 AHNAK2 gene encodes a large nucleoprotein that may play a role in calcium signaling by associating with calcium channel proteins. [38]
Zhang, et al. 2016 [40] ALOX5AP rs12876893 Asain 5 (MG) G<A 1.12 (1.06–1.180) 6.20×10-5 ALOX5AP gene encodes a protein which is required for leukotriene synthesis. ALOX5AP is expressed in airway leukocytes in response to stimuli implicated in various inflammatory responses including asthma, arthritis and psoriasis. [38,40]
Molineros, et al. 2017 [41] ANKS1A rs2762340 Overall 9 (MG) G<A 0.87 (0.84–0.90) 4.93×10-15 ANKS1A, also known as ODIN, a Src kinase that negatively regulates growth factor receptor signaling pathways. ANKS1Ainteracts with and is phosphorylated by Lck (lymphocyte-specific protein tyrosine kinase), a critical component of T-cell activation. [41]
Bentham, et al. 2015 [35] ARID5B rs4948496 European 2 (MG) C<T 1.14 (1.10–1.19) 1.04×10-10 The encoded protein forms a histone H3K9Me2 demethylase complex with PHD finger protein 2 and regulates the transcription of target genes involved in adipogenesis and liver development. This gene also plays a role in cell growth and differentiation of B-lymphocyte progenitors. [38]
Molineros, et al. 2017 [41] ATG16L2 rs11235604 Asian 8 (MG) T<C 0.78 (0.71–0.85) 8.87×10-12 An autophagy-related gene associated with systemic lupus erythematosus (SLE), multiple sclerosis, and Crohn disease. ATG16L2 is involved in apoptosis and physically interacts with SLE locus ATG5.
Morris, et al. 2016 [42] ATXN1 rs17603856 Overall 3 (MG) T<G 0.88 (0.85–0.91) 3.27×10-12 ATXN1 binds RNA and several transcription factors, and is involved in transcriptional regulation. [43] The diseased allele of ATXN1 with the expansion of CAG repeats is associated with spinocerebellar ataxia type 1. [38]
Morris, et al. 2016 [42] BACH2 rs597325 Overall 3 (MG) G<A 0.89 (0.86–0.92) 4.03×10-12 A transcription regulator protein. BACH2 is expressed in primary B cells. BACH2 protein play important role as transcriptional activators or repressors. [44] The superenhancer associated genes critical for T-cell biology are repressed by BACH2. [45]
Bentham, et al. 2015 [35] BANK1 rs10028805 European 2 (MG) G<A 1.20 (1.15–1.25) 4.31×10-17 BANK1 encodes a protein adaptor that is predominantly expressed in B cells. It promotes LYN-mediated tyrosine phosphorylation of inositol 1,4,5-triphosphate receptors. [46]
Lee, et al. 2012 [47] BLK rs13277113 European 2 (MG) A<G 1.391 (1.256–1.540) 2.28×10-10 BLK gene encodes a nonreceptor tyrosine kinase of the Src family of proto-oncogenes that are typically involved in cell proliferation and differentiation. The protein has a role in B-cell receptor signaling and B-cell development. [38]
Bentham, et al. 2015 [35] BLK rs2736340 European 2 (MG) T<C 1.29 (1.22–1.37) 6.28×10-20
Molineros, et al. 2017 [41] CCL22 rs223881 Overall 9 (MG) C<T 0.87 (0.84–0.90) 5.87×10-16 CCL22 is a Cys-Cys (CC) cytokine gene. The encoded cytokine displays chemotactic activity for monocytes, dendritic cells (DCs), natural killer cells, and chronically activated T lymphocytes. It binds to chemokine receptor CCR4. [38]
Lee, et al. 2015 [48] CD40 rs4810485 European 2 (MO) TT vs. TG+GG 0.339 (0.205–0.508) 1.7×10-8 The encoded protein of CD40 gene is a receptor on antigenpresenting cells of the immune system and is essential for mediating a broad variety of immune responses including T-cell-dependent immunoglobulin class switching, memory B-cell development, and germinal center formation. [38]
Lessard, et al. 2011 [49] CD44 rs387619 European (MG) C<T 0.82 (0.76–0.88) 1.46×10-8 The protein encoded by the CD44 gene is a cell-surface glycoprotein involved in cell-cell interactions, cell adhesion and migration. This protein participates in a wide variety of cellular functions including lymphocyte activation, recirculation and homing, hematopoiesis, and tumor metastasis. [38]
Sheng, et al. 2015 [50] CD44 rs2732547 Chinese 3 (MG) G<A 0.82 (0.77–0.87) 1.55×10-11
Bentham, et al. 2015 [35] CD44 rs2732549 European 2 (MG) T<C 1.24 (1.19–1.29) 1.20×10-23
Lessard, et al. 2011 [49] CD44 rs2732552 European (MG) C<T 0.82 (0.76–0.88) 1.82×10-9
Zhang, et al. 2016 [40] CD80 rs2222631 Asain 5 (MG) A<G 0.86 (0.81–0.91) 4.50×10-8 The protein encoded by the CD80 gene is a membrane receptor that is activated by the binding of CD28 or CTLA-4. The activated protein induces T-cell proliferation and cytokine production. [38]
Sheng, et al. 2015 [50] CD80 rs6804441 Chinese 3 (MG) G<A 0.86 (0.82–0.91) 5.90×10-4
Bentham, et al. 2017 [35] CFB rs1270942 European 2 (MG) G<A 2.28 (2.15–2.42) 2.25×10-165 CFB gene encodes complement factor B, a component of the alternative pathway of complement activation. [38]
Bentham, et al. 2017 [35] CIITA-SOCS1 rs9652601 European 2 (MG) A<G 1.21 (1.15–1.26) 7.42×10-17 CIITA gene encodes a protein with an acidic transcriptional activation domain, 4 LRRs (leucine-rich repeats) and a guanosine triphosphate binding domain. The protein acts as a positive regulator of class II major histocompatibility complex gene transcription. [38] SOCS1 gene encodes a member of the signal transducer and activator of transcription (STAT)-induced STAT inhibitor (SSI) family, also known as suppressor of cytokine signaling. It takes part in a negative feedback loop to attenuate cytokine signaling. [38]
Bentham, et al. 2017 [35] CSK rs2289583 European 2 (MG) A<C 1.19 (1.14–1.24) 6.22×10-15 The protein encoded by the CSK gene is involved in multiple pathways, including the regulation of Src family kinases. It plays an important role in T-cell activation through its association with the protein encoded by the protein tyrosine phosphatase, nonreceptor type 22 (PTPN22) gene. An intronic polymorphism (rs34933034) in this gene has been found to affect B-cell activation and is associated with SLE. [38]
Shojaa, et al. 2017 [51] CTLA-4 rs733618 Overall 8 (MO) TT vs. CC 2.32 (1.62–3.32) <0.001 CTLA-4 gene is a member of the immunoglobulin superfamily and encodes a protein which transmits an inhibitory signal to T cells. [38]
Zhang, et al. 2017 [52] CXCR5 rs10892301 Asian 3 (MG) A<G 0.85 (0.80–0.90) 2.51×10-8 CXCR5 gene encodes a multipass membrane protein that belongs to the CXC chemokine receptor family. This cytokine receptor is involved in B-cell migration into B-cell follicles of spleen and Peyer patches. [38]
Bentham, et al. 2017 [35] CXorf21 rs887369 European 2 (MG) A<C 1.15 (1.10–1.21) 5.26×10-10 A protein coding gene of unknown function. [53]
Lessard, et al. 2017 [39] DOCK1 rs10901656 Asian 2 (MG) T<C 1.21 (1.12–1.32) 9.56×10-6 DOCK1 gene encodes a member of the dedicator of cytokinesis protein family. Dedicator of cytokinesis proteins regulates the small GTPase Rac, thereby influencing several biological processes, including phagocytosis and cell migration. [38]
Wang, et al. 2017 [54] ETS1 rs6590330 Caucasian 3 (MG) A<G 1.22 (1.10–1.34) 9.8×10-5 ETS1 gene encodes for a transcription factor known to be involved in a wide range of immune functions, including Th17 cell development and terminal differentiation of B lymphocytes. [55]
Bentham, et al. 2017 [35] ETS1-FLI1 rs7941765 European 2 (MG) T<C 1.14 (1.10–1.19) 1.35×10-10 FLI1 gene encodes a transcription factor containing an ETS DNA-binding domain. [38]
Lee, et al. 2017 [47] FAM167A rs12680762 European 2 (MG) A<G 1.335 (1.208–1.475) 1.45×10-8 FAM167A gene is a ubiquitously expressed gene of unknown function.
Bentahm, et al. 2017 [35] FCGR2A rs1801274 European 2 (MG) C<T 1.16 (1.11–1.21) 1.04×10-12 FCGR2A gene encodes a cell-surface receptor found on phagocytic cells such as macrophages and neutrophils, and is involved in the process of phagocytosis and clearing of immune complexes. [38]
Zhu, et al. 2017 [56] FCGR2B rs1050501 Overall 12 (MO) CC vs. CT+TT 1.754 (1.422–2.165) 1.61×10-7 FCGR2B is an immunoreceptor tyrosine-based inhibitory motif (ITIM)-containing receptor and it mediates both endocytotic and apoptotic signaling on B cells and myelomonocytic cells.
Zhu, et al. 2017 [56] FCGR3A rs396991 Overall 26 (MO) TT vs. TG+GG 1.263 (1.123–1.421) 9.62×10-5 FCGR3A gene is involved in the removal of antigen-antibody complexes from the circulation, as well as other antibodydependent responses. The encoded receptor is expressed on natural killer (NK) cells. [38]
Lessard, et al. 2017 [39] FCHSD2-P2RY2 rs11235667 Asian 2 (MG) G<A 0.63 (0.55–0.72) 6.67×10-11 FCHSD2 gene has been described as regulator of F-actin assembly through interactions with WAS (also known as WASP) and WASL (also known as N-WASP). WAS plays an important role in the migration of T cells through reorganization of the actin cytoskeleton subsequent to interactions with dendritic or B cells. P2RY2 is a receptor for adenosine triphosphate (ATP) and uridine triphosphate (UTP) that acts as a sensor for the release of nucleotides by apoptotic cells. It is also known to induce CCL2 secretion in macrophages.
Sheng, et al. 2017 [50] FLJ25996 rs9866504 Chinese 3 (MG) G<A 0.85 (0.79–0.92) 6.44×10-2 No information
Sheng, et al. 2017 [50] GPM6A rs997779 Chinese 3 (MG) G<A 1.17 (1.08–1.26) 4.48×10-2 GPM6A gene is abundant in all rat hippocampal subregions, and it localized to membrane protrusions (filopodia/spines) of primary hippocampal neurons. This gene has a role in neurite/filopodium outgrowth and synapse formation.
Lessard, et al. 2017 [39] GTF2IRD1 rs2267828 Asian 2 (MG) G<A 0.81 (0.76–0.88) 6.46×10-8 The protein encoded by this gene contains 5 GTF2I-like repeats and each repeat possesses a potential helix-loop-helix (HLH) motif. It may interact with other HLH-proteins and function as a transcription factor or as a positive transcriptional regulator under the control of Retinoblastoma protein. This gene plays a role in craniofacial and cognitive development. [38]
Morris, et al. 2016 [42] GTF2IRD1-GTF2I rs73135369 Overall 3 (MG) C<T 1.32 (1.23–1.42) 8.77×10-14 This gene encodes a phosphoprotein containing 6 characteristic repeat motifs. The encoded protein binds to the initiator element (Inr) and E-box element in promoters and functions as a regulator of transcription. [38]
Zhang, et al. 2015 [57] HCFC1 rs17422 Asian 2 (MG) T<C 0.75 (0.71–0.80) 1.47×10-15 This gene is a member of the host cell factor family and encodes a protein with 5 Kelch repeats, a fibronectin-like motif, and 6 HCF repeats, each of which contains a highly specific cleavage signal. It is involved in control of the cell cycle and transcriptional regulation during herpes simplex virus infection. [38]
Niu, et al. 2015 [58] HLA-DR3 Overall 17 (MO) DR3 1.88 (1.58–2.23) <0.001 Major histocompatibility complex, class II, DR beta 1 (HLA-DRB1 gene).
The HLA-DRB1 locus is ubiquitous and encodes a very large number of functionally variable gene products (HLA-DR1 to HLA-DR17). HLA-DRB1 belongs to the HLA class II beta chain paralogs. It plays a central role in the immune system by presenting peptides derived from extracellular proteins. Class II molecules are expressed in antigen-presenting cells (APC: B lymphocytes, DCs, macrophages). [38]
Niu, et al. 2015 [58] HLA-DR11 Overall 15 (MO) DR11 0.72 (0.60–0.85) <0.0001
Castaño-Rodríguez, et al. 2008 [59] HLA-DR2 Latin American 9 (MO) DR2 1.754 (1.404–2.191) 0
Lee, et al. 2015 [60] HLA-G rs1063320 Overall 4 (MO) G vs. C 1.367 (1.158–1.613) 2.2×10-5 HLA-G belongs to the HLA class I heavy chain paralogs. [38] Nonclassic HLA-G class I molecules inhibit natural killer cell function. [61]
Kim, et al. 2012 [62] ICAM1–ICAM4–ICAM5 rs3093030 Overall 4 (MO) A vs. G 1.16 (1.11–1.22) 4.88×10-10 ICAM1 gene encodes a cell-surface glycoprotein which is mainly expressed in the vascular endothelium, macrophages and lymphocytes, and plays a role in immunological events including extravasation and T-cell-mediated responses. ICAM4 gene encodes the Landsteiner-Wiener blood group antigen(s) that belongs to the immunoglobulin (Ig) superfamily. It contains 2 Ig-like C2-type domains and binds to the leukocyte adhesion LFA-1 protein. ICAM5 is preferentially expressed in brain.
Bentham, et al. 2015 [35] IFIH1 rs2111485 European 2 (MG) C<G 1.15 (1.11–1.20) 1.27×10-11 IFIH1 gene encodes a DEAD box protein that is upregulated in response to treatment with beta-interferon and a protein kinase C-activating compound, mezerein.
The encoded protein participates in the activation of apoptosis in viral dsRNA infected cells, modulating type 1 interferon (IFN) response, production of proinflammatory cytokines and apoptotic processes. [63]
Morris, et al. 2016 [42] IKBKE rs2297550 Overall 3 (MG) G<C 1.16 (1.11–1.21) 1.31×10-11 IKBKE is a noncanonical I-kappa-B kinase that is essential for regulating antiviral signaling pathways.
Bentham, et al. 2015 [35] IKZF1 rs4917014 European 2 (MG) G<T 1.18 (1.13–1.24) 6.39×10-14 IKZF1 gene encodes a transcription factor associated with chromatin remodeling. It functions as a regulator of lymphocyte differentiation. [38]
Bentham, et al. 2015 [35] IKZF2 rs3768792 European 2 (MG) G<A 1.24 (1.17–1.31) 1.21×10-13 IKZF2 gene encodes a member of the Ikaros family of zincfinger proteins that is involved in the regulation of lymphocyte development. [38]
Bentham, et al. 2015 [35] IKZF3 rs2941509 European 2 (MG) T<C 1.35 (1.22–1.49) 7.98×10-9 IKZF3 gene encodes a member of the Ikaros family of zincfinger proteins. This gene product is a transcription factor that is important in the regulation of B-lymphocyte proliferation and differentiation. [38]
Bentham, et al. 2015 [35] IL-10 rs3024505 European 2 (MG) A<G 1.17 (1.11–1.24) 4.64×10-9 Interleukin (IL)-10 is produced primarily by monocytes and to a lesser extent by lymphocytes. It down-regulates the expression of Th1 cytokines, major histocompatibility complex (MHC) class II Ags, and costimulatory molecules on macrophages. It enhances B-cell survival, proliferation, and antibody production. It can block NF-kappa B activity, and is involved in the regulation of the Janus kinase (JAK)-STAT signaling pathway. [38]
Bentham, et al. 2015 [35] IL-12A rs564799 European 2 (MG) C<T 1.14 (1.09–1.18) 1.54×10-9 IL-12A acts on T and natural killer cells. It is required for the T-cell-independent induction of IFN-gamma, and is important for the differentiation of both Th1 and Th2 cells. [38]
Qi, et al. 2015 [64] IL-21 rs907715 Overall 7 (MO) GG+GA vs. AA 1.20 (1.09–1.31) 0 IL-21 plays a role in both the innate and adaptive immune responses by inducing the differentiation, proliferation and activity of multiple target cells including macrophages, natural killer cells, B cells and cytotoxic T cells. [38]
Ryan, et al. 2009 [65] IL-21R rs3093301 Overall 2 (MO) A vs. G 1.16 (1.08–1.25) 1.0×10-4 IL-21R gene encodes a cytokine receptor for IL-21. It transduces the growth promoting signal of IL21, and is important for the proliferation and differentiation of T cells, B cells, and NK cells. [38]
Katkam, et al. 2017 [66] IL-6 rs1800797 Overall 13 (MO) G vs. C 1.36 (1.22–1.53) 0.00 IL-6 functions in inflammation and the maturation of B cells. In addition, it has been shown to be an endogenous pyrogen capable of inducing fever in people with autoimmune diseases or infections. [38]
Zhang, et al. 2015 [57] IRAK1 rs1059702 Asian 2 (MG) C<T 0.71 (0.67–0.76) 2.40×10-18 IRAK1 gene encodes the interleukin-1 receptor-associated kinase 1. It is partially responsible for IL1-induced upregulation of the transcription factor NF-kappa B. [38]
Bentham, et al. 2015 [35] IRF5 rs10488631 European 2 (MG) C<T 1.92 (1.81–2.03) 9.37×10-110 Proteins of the interferon regulatory factor (IRF) family bind to the IFN-stimulated response element and regulate expression of genes stimulated by type I IFNs, namely IFN-alpha and IFN-beta. IRF family proteins also control expression of IFNalpha and IFN-beta-regulated genes that are induced by viral infection. [38]
Lee, et al. 2012 [47] IRF5 rs729302 European 2 (MG) C<A 0.774 (0.707–0.848) 3.93×10-8
Bentham, et al. 2015 [35] IRF7 rs12802200 European 2 (MG) A<C 1.23 (1.15–1.31) 8.81×10-10
Bentham, et al. 2015 [35] IRF8 rs11644034 European 2 (MG) A<G 1.25 (1.19–1.32) 9.58×10-18
Sheng, et al. 2015 [50] IRF8 rs2934498 Chinese 2 (MG) G<A 1.25 (1.16–1.34) 4.97×10-9
Bentham, et al. 2015 [35] ITGAM rs34572943 European 2 (MG) A<G 1.71 (1.61–1.81) 3.39×10-76 ITGAM gene encodes the integrin alpha M chain. It is important in the adherence of neutrophils and monocytes to stimulated endothelium, and also in the phagocytosis of complement coated particles. [38]
Morris, et al. 2016 [42] JAK2 rs1887428 Overall 3 (MG) G<C 1.16 (1.12–1.20) 2.19×10-17 JAK2 encodes a tyrosine kinase involved in a specific subset of cytokine receptor signaling pathways. It has been found to be associated with the prolactin receptor and is required for responses to gamma interferon. [38]
Bentham, et al. 2015 [35] JAZF1 rs849142 European 2 (MG) C<T 1.14 (1.10–1.19) 8.61×10-11 JAZF1 gene encodes a nuclear protein that functions as a transcriptional repressor. [38]
Zhang, et al. 2015 [57] L1CAM rs4898457 Asian 2 (MG) G<A 0.87 (0.82–0.92) 2.84×10-6 L1CAM gene encodes an axonal glycoprotein belonging to the immunoglobulin supergene family. This cell adhesion molecule plays an important role in nervous system development, including neuronal migration and differentiation. [38]
Morris, et al. 2016 [42] LBH rs17321999 Overall 3 (MG) A<C 0.83 (0.79–0.87) 2.22×10-16 LBH (limb bud and heart development) is a key gene regulator which could act as a transcriptional coactivator in the mitogen ‐activated protein kinase signaling pathway to mediate cellular functions. Several SNP within LBH are associated with rheumatoid arthritis and SLE. [67]
Morris, et al. 2016 [42] LBH rs7579944 Overall 3 (MG) C<T 0.90 (0.87–0.93) 1.41×10-9
Morris, et al. 2016 [42] LPP-TPRG1-AS1 rs6762714 Overall 3 (MG) C<T 1.16 (1.12–1.20) 4.00×10-15 LPP gene encodes a protein localizes to the cell periphery in focal adhesions and may be involved in cell-cell adhesion and cell motility. It also functions as a transcriptional coactivator. [38]
Wang, et al. 2013 [54] LRRC18-WDFY4A rs1913517 Caucasian 3 (MG) A<G 1.16 (1.08 –1.23) 7.8×10-6 Both LRRC18 and WDFY4 are of unknown function.
Bentham, et al. 2015 [35] LYST rs9782955 European 2 (GWAS) T<C 1.16 (1.11–1.22) 1.25×10-9 LYST gene encodes a protein that regulates intracellular protein trafficking in endosomes, and may be involved in pigmentation. [38] No known immune function. Studies have revealed that LYST functions in lysosomal trafficking in many immune cells, a process that is also crucial in the activation of TLRs by self-nucleic acids in SLE. [68]
Lee, et al. 2012 [69] MBL2 rs1800450 Overall 21 (MO) B vs. A 1.298 (1.154–1.459) 1.49×10-5 MBL2 gene encodes the soluble mannose-binding lectin or protein. It recognizes mannose and N-acetylglucosamine on many microorganisms, and is capable of activating the classical complement pathway. [38]
Bentham, et al. 2015 [35] MECP2 rs1734787 European 2 (MG) C<A 1.31 (1.22–1.40) 1.78×10-15 MECP2 is a dichotomous transcriptional regulator that either activates or represses gene expression. [70]
Zhang, et al. 2015 [57] MECP2 rs2734647 Asian 2 (MG) C<T 0.72 (0.67–0.76) 5.22×10-18
Bentham, et al. 2015 [35] miR-146a rs2431697 European 2 (MG) C<T 1.26 (1.21–1.31) 8.01×10-28 MicroRNA 146a can repress type 1 IFN pathway through targeting TNF receptor-associated factor 6, IL-1 receptorassociated kinase, IFN regulator factor 5 (IRF5), and STAT-1. [71]
Molineros, et al. 2017 [41] MYNN rs10936599 Overall 9 (MG) C<T 1.14 (1.10–1.18) 1.92×10-13 MYNN encodes the zinc-finger transcription factor myoneurin, which regulates neuromuscular junctions and telomere length. [41]
Zhang, et al. 2015 [57] NAA10 rs1557501 Asian 2 (MG) C<T 0.83 (0.79–0.88) 7.84×10-10 NAA10 gene encodes an N-terminal acetyltransferase that functions as the catalytic subunit of the major amino-terminal acetyltransferase A complex. [38]
Zhang, et al. 2015 [57] NAA10 rs2071128 Asian 2 (MG) G<A 0.81 (0.77–0.86) 2.19×10-13
Bentham, et al. 2015 [35] NADSYN1 rs3794060 European 2 (MG) T<C 1.23 (1.18–1.29) 1.32×10-20 This gene encodes a synthetase that catalyzes the final step in the biosynthesis of Nicotinamide adenine dinucleotide.
Zhang, et al. 2015 [57] Near-VCX2 rs5978830 Asian 2 (MG) A<G 0.84 (0.80–0.89) 1.00×10-8 This gene belongs to the VCX/Y gene family, which has multiple members on both X and Y chromosomes that are expressed exclusively in male germ cells. The VCX gene cluster is polymorphic in terms of copy number; different individuals may have a different number of VCX genes. This gene contains 2 copies of a 30 nt tandem repeat. Deletion of a nearby member of this family was implicated in cognitive disability. [38]
Sheng, et al. 2015 [50] NRXN1 rs2048979 Chinese 3 (MG) G/A 0.87 (0.82–0.91) 1.35×10-3 Neurexins are cell-surface receptors that bind neuroligins to form Ca(2+)-dependent neurexin/neuroligin complexes at synapses in the central nervous system. This complex is required for efficient neurotransmission and is involved in the formation of synaptic contacts. [38]
Lee, et al. 2017 [72] OPN rs11229919 Asian 2 (MO) C vs. T 2.070 (1.570–2.730) 2.5×10-7 The protein encoded by this gene is involved in the attachment of osteoclasts to the mineralized bone matrix. It is also a cytokine that upregulates expression of interferon-gamma and interleukin-12. [38]
Zhang, et al. 2014 [52] PHLDB1 rs11603023 Asian 3 (MG) T<C 1.20 (1.12–1.27) 1.25×10-8 PHLDB1 is an insulin responsive protein that enhances AKT activation. AKT signaling pathway plays an important role in cellular proliferation and growth signaling. Abnormal activation of the AKT signaling pathway was found in peripheral blood T cells from individuals with SLE. [52]
Bentham, et al. 2015 [35] PLD2 rs2286672 European 2 (MG) T<C 1.25 (1.16–1.35) 2.93×10-9 The protein encoded by this gene catalyzes the hydrolysis of phosphatidylcholine to phosphatidic acid and choline. This protein localizes to the peripheral membrane and may be involved in cytoskeletal organization, cell cycle control, transcriptional regulation, and/or regulated secretion. [38]
Tan, et al. 2011 [73] PPP2CA rs10491322 Overall 4 (MO) G vs. A 1.2 (1.07–1.27) 3.8×10-4 PPP2CA gene encodes the phosphatase 2A catalytic subunit. Protein phosphatase 2A is implicated in the negative control of cell growth and division. [38]
Tan, et al. 2011 [73] PPP2CA rs7704116 Overall 4 (MO) A vs. G 1.3 (1.14–1.31) 3.8×10-7
Bentham, et al. 2015 [35] PRDM1-ATG5 rs6568431 European 2 (MG) A<C 1.21 (1.15–1.27) 5.04×10-14 PRDM1 gene encodes a protein that acts as a repressor of beta-interferon gene expression. [38] The encoded protein by ATG5 gene is involved in several cellular processes, including autophagic vesicle formation, mitochondrial quality control after oxidative damage, negative regulation of the innate antiviral immune response, lymphocyte development and proliferation, MHC II antigen presentation, adipocyte differentiation, and apoptosis. [38]
Bentham, et al. 2015 [35] PTPN22 rs2476601 European 2 (MG) T<C 1.43 (1.34–1.53) 1.10×10-8 PTPN22 gene encodes a lymphoid-specific intracellular phosphatase that associates with the molecular adapter protein CBL and may be involved in regulating CBL function in the T-cell receptor signaling pathway. [38]
Morris, et al. 2016 [42] PTPRC rs34889541 Overall 3 (MG) A<G 0.81 (0.76–0.86) 2.44×10-12 The protein encoded by this gene is a member of the protein tyrosine phosphatase (PTP) family. PTPs are known to be signaling molecules that regulate a variety of cellular processes including cell growth, differentiation, mitosis, and oncogenic transformation. PTP is also an essential regulator of T- and B-cell antigen receptor signaling. [38]
Ramos, et al. 2011 [74] PXK rs6445975 Overall 4 (MG) G<T 1.20 (1.13–1.27) 5.27×10-9 This gene encodes a phox (PX) domain-containing protein which may be involved in synaptic transmission and the ligand-induced internalization and degradation of epidermal growth factors. [38]
Bentham, et al. 2015 [35] RAD51B rs4902562 European 2 (MG) A<G 1.14 (1.09–1.19) 6.15×10-10 RAD51 family members are evolutionarily conserved proteins essential for DNA repair by homologous recombination. Overexpression of this gene was found to cause cell cycle G1 delay and cell apoptosis, which suggested a role of this protein in sensing DNA damage. [38]
Molineros, et al. 2017 [41] RNASEH2C rs1308020 Overall 9 (MG) T<C 0.84 (0.81–0.88) 2.96×10-19 RNASEH2C encodes subunit C of the human ribonuclease H2 enzyme complex that trims RNA-DNA duplexes.
Morris, et al. 2016 [42] RNASEH2C rs494003 Overall 3 (MG) A<G 1.14 (1.09–1.19) 5.81×10-9
Bentham, et al. 2015 [35] SH2B3 rs10774625 European 2 (MG) A<G 1.13 (1.08–1.18) 4.09×10-9 The encoded protein is a key negative regulator of cytokine signaling and plays a critical role in hematopoiesis. [38] Functional analysis indicated that it inhibits the activation of NFAT in stimulated T cells. [75]
Bentham, et al. 2015 [35] SLC15A4 rs1059312 European 2 (MG) G<A 1.17 (1.12–1.21) 1.48×10-13 SLC15A4 belongs to a superfamily of proton-coupled oligopeptide transporters. [76] Kobayashi et al. [77] (2014) found that B-cell-derived Slc15a4 was crucial for Tlr7 (300365)-triggered type I interferon (e.g., IFNA) and autoantibody production in a mouse model of lupus (SLE).
Bentham, et al. 2015 [35] SMG7-NCF2 rs17849501 European 2 (MG) T<C 2.10 (1.95–2.26) 3.45×10-88 SMG7 gene encodes a protein that is essential for nonsensemediated mRNA decay; a process whereby transcripts with premature termination codons are targeted for rapid degradation by a mRNA decay complex. NCF2 gene encodes neutrophil cytosolic factor 2, the cytosolic subunit of the multiprotein nicotinamide adenine dinucleotide phosphate oxidase complex found in neutrophils. It produces a burst of superoxide which is delivered to the lumen of the neutrophil phagosome. [38]
Lee, et al. 2012 [47] STAT4 rs10931481 European 2 (MG) A<G 1.312 (1.194–1.442) 1.74×10-8 STAT4 encodes a member of the STAT family of transcription factors. In response to cytokines and growth factors, it acts as transcription activator. This protein is essential for mediating responses to IL12 in lymphocytes, and regulating the differentiation of T helper cells. [38]
Bentham, et al. 2015 [35] STAT4 rs11889341 European 2 (MG) T<C 1.73 (1.65–1.81) 5.59×10-122
Lee, et al. 2012 [47] STAT4 rs7574865 European 2 (MG) T<G 1.477 (1.335–1.634) 4.06×10-14
Bentham, et al. 2015 [35] TCF7-SKP rs7726414 European 2 (MG) T<C 1.45 (1.32–1.58) 4.44×10-16 TCF7 is a T-cell-specific transcription factor that regulates the expression of CD3. plays a critical role in natural killer cell and innate lymphoid cell development. [38]
Lee, et al. 2016 [78] TLR7 rs3853839 Asian 3 (MO) allele 2 vs. allele 1 0.773 (0.725–0.823) <1.0×10-9 The protein encoded by this gene is a member of the Toll-like receptor family which plays a fundamental role in pathogen recognition and activation of innate immunity. [38]
Zhang, et al. 2015 [57] TMEM187 rs2266888 Asian 2 (MG) G<A 0.76 (0.72–0.81) 8.20×10-15 This gene consists of 2 exons and encodes a multipass membrane protein. An alternatively spliced transcript variant encoding the same protein has been found, but its biological validity is not determined. [38]
Zhang, et al. 2015 [57] TMEM187 rs6571303 Asian 2 (MG) C<T 0.80 (0.76–0.84) 3.06×10-13
Sheng, et al. 2015 [50] TMEM39A rs12494314 Chinese 3 (MG) C<T 0.84 (0.80–0.89) 1.01×10-9 The TMEM39A-associated coding SNP (rs1132200) results in an amino acid change from alanine to threonine at position 487 of the protein. Although almost no biological data have been published suggesting its relevance to SLE, it has been found to be associated with multiple sclerosis. [79]
Bates, et al. 2009 [80] TNFAIP3 rs5029939 Caucasian 2 (MG) G<T 2.09 (1.68–2.60) 1.67×10-14 The tumor necrosis factor alpha inducible protein 3 (TNFAIP3) encodes the ubiquitin-modifying enzyme A20 and is an inhibitor of nuclear factor-kB activity in several signaling pathways, including those of TNF and Toll-like receptors. Also, it is required for the negative regulation of inflammatory responses. [81]
Bentham, et al. 2015 [35] TNFAIP3 rs6932056 European 2 (MG) C<T 1.83 (1.65–2.02) 1.97×10-31
Ramos, et al. 2011 [74] TNFSF4 rs10798269 Overall 4 (MG) A<G 0.83 (0.78–0.88) 4.04×10-10 TNFSF4 gene encodes a cytokine of the TNF ligand family. The encoded protein functions in T-cell APC interactions and mediates adhesion of activated T cells to endothelial cells. [38]
Sheng, et al. 2015 [50] TNFSF4 rs1418190 Chinese 2 (MG) C<T 0.81 (0.75–0.87) 1.08×10-8
Sheng, et al. 2015 [50] TNFSF4 rs4916219 Chinese 2 (MG) A<G 0.80 (0.75–0.86) 7.77×10-9
Bentham, et al. 2015 [35] TNFSF4 rs704840 European 2 (MG) G<T 1.22 (1.17–1.27) 3.12×10-9
Yang, et al. 2017 [82] TNF-α rs1800629 Overall 41 (MO) A vs. G 1.70 (1.46–1.98) <0.001 TNF is a pleiotropic cytokine that produces different stimuli in various physiological and pathological conditions. TNF contributes importantly to the development of T cells, B cells, and DCs. [47]
Bentham, et al. 2015 [35] TNIP1 rs10036748 European 2 (MG) C<T 1.38 (1.32–1.45) 1.27×10-45 TNIP1 gene encodes an A20-binding protein which plays a role in autoimmunity and tissue homeostasis through the regulation of nuclear factor kappa-B activation. [38]
Wang, et al. 2013 [54] TNIP1 rs7708392 Caucasian 3 (MG) C/G 1.29 (1.17–1.44) 1.2×10-6
Lee, et al. 2012 [47] TNPO3 rs12531711 European 2 (MG) G<A 1.593 (1.403–1.808) 6.41×10-13 TNPO3 is a nuclear import receptor for serine/argininerich (SR) proteins, which are essential precursor-mRNA splicing factors. [83]
Kurreeman, et al. 2010 [84] TRAF1-C5 rs10818488 Overall 3 (MG) A 1.22 (1.12–1.31) 1.02×10-6 TRAF1 is involved in the negative regulation of T-cell proliferation and serves as an essential effector of the TNF signaling cascade. C5 is known to be a factor in the complement cascade and may increase susceptibility to autoimmune and inflammatory disease. [85]
Namjou, et al. 2012 [86] TRAF6 rs4755453 Overall 4 (MO) C vs. G 0.88 (0.83–0.94) 4.73×10-5 TRAF6 encodes an adaptor molecule that has a central role in the nuclear factor NF-κB activation pathway. It regulates inflammation, DC development, thymic selection and regulatory T-cell production as well as osteoclast formation.
Namjou, et al. 2012 [86] TRAF6 rs5030437 Overall 4 (MO) A vs. G 0.88 (0.83–0.94) 7.85×10-5
Namjou, et al. 2012 [86] TRAF6 rs5030445 Overall 4 (MO) A vs. G 0.88 (0.83–0.94) 1.31×10-4
Namjou, et al. 2012 [86] TRAF6 rs5030472 Overall 4 (MO) A vs. G 0.85 (0.77–0.92) 4.75×10-4
Bentham, et al. 2015 [35] TYK2 rs2304256 European 2 (MG) A<C 1.24 (1.17–1.31) 3.50×10-13 TYK2 gene encodes a member of the tyrosine kinase and, more specifically, the JAKs protein families. This protein associates with the cytoplasmic domain of type I and type II cytokine receptors and promulgate cytokine signals by phosphorylating receptor subunits. It is also component of both the type I and type III interferon signaling pathways. [38]
Diaz-Gallo, et al. 2013 [87] UBASH3a rs9976767 Overall 2 (MO) G vs. A 1.23 (1.11–1.37) 2.4×10-4 UBASH3 gene encodes one of 2 family members belonging to the T-cell ubiquitin ligand family. Both family members can negatively regulate T-cell signaling. [38]
Ramos, et al. 2011 [74] UBE2L3 rs181359 Overall 4 (MG) T<C 1.23 (1.15–1.33) 1.15×10-9 The modification of proteins with ubiquitin is an important cellular mechanism for targeting abnormal or shortlived proteins for degradation. This gene encodes a member of the E2 ubiquitin-conjugating enzyme family. It participates in the ubiquitination of p53, c-Fos, and the NF-kB precursor p105 in vitro. [38] UBE2L3 participates in ubiquitylation and has a key role in the regulation of innate and adaptive immune systems. [88]
Bentham, et al. 2015 [35] UBE2L3 rs7444 European 2 (MG) T<C 1.27 (1.21–1.33) 1.84×10-22
Bentham, et al. 2015 [35] UHRF1BP1 rs9462027 European 2 (MG) A<G 1.14 (1.09–1.19) 7.55×10-9 UHRF1 binding protein 1
Sheng, et al. 2015 [50] ULK3 rs881536 Chinese 2 (MG) A/C 1.16 (1.07–1.23) 5.78×10-3 The kinase domain of ULK3 was required for reporter activation. ULK3 showed autophosphorylation activity, and it showed serine/threonine kinase activity toward GLI2, with lower kinase activity toward GLI1 and GLI3. [89]
Zhou, et al. 2014 [90] VDRr rs2228570 Overall 6 (MO) F vs. F 0.75 (0.65–0.86) <0.0001 VDRr gene encodes vitamin D3 receptor, which is a member of the nuclear hormone receptor superfamily of ligand-inducible transcription factors. Downstream targets of vitamin D3 receptor are principally involved in mineral metabolism, though this receptor regulates a variety of other metabolic pathways, such as those involved in immune response and cancer. [38]
Bentham, et al. 2015 [35] WDFY4 rs2663052 European 2 (MG) G<A 1.16 (1.10–1.22) 5.25×10-9 WDFY4 is a huge protein with unknown function but is predominantly expressed in primary and secondary immune tissues.
Zhang, et al. 2015 [91] YDJC rs2298428 Overall 3 (MG) T<C 1.23 (1.16–1.3) 1.31×10-11 The role of the YDJC gene is currently largely unknown. [88]
Morris, et al. 2016 [42] ZFP90 rs1170426 Overall 3 (MG) C 1.12 (1.08–1.17) 2.24×10-8 ZFP90 gene encodes a member of the zinc-finger protein family that modulates gene expression. The encoded protein derepresses the transcription of certain fetal cardiac genes and may contribute to the genetic reprogramming that occurs during the development of heart failure. [38]

OR, odds ratio; CI, confidence interval; MG, meta-analysis of genome-wide association studies; MO, meta-analysis of observation studies.